Guarda come risolvere il Sudoku difficile. Come risolvere il Sudoku: modi, metodi e strategia
Il campo Sudoku è una tabella di 9x9 celle. In ogni cella viene inserito un numero da 1 a 9. Lo scopo del gioco è disporre i numeri in modo tale che non ci siano ripetizioni in ogni riga, in ogni colonna e in ogni blocco 3x3. In altre parole, ogni colonna, riga e blocco deve contenere tutti i numeri da 1 a 9.
Per risolvere il problema, puoi scrivere i candidati nelle celle vuote. Consideriamo ad esempio la cella della 2a colonna della 4a riga: la colonna in cui si trova ha già i numeri 7 e 8, la riga ha i numeri 1, 6, 9 e 4, il blocco ha 1, 2, 8 e 9 Pertanto, dai candidati in questa cella cancelliamo 1, 2, 4, 6, 7, 8, 9 e rimaniamo con solo due possibili candidati: 3 e 5.

Allo stesso modo, consideriamo possibili candidati per altre celle e otteniamo la seguente tabella:

È più interessante decidere con i candidati e puoi utilizzare vari metodi logici. Successivamente ne esamineremo alcuni.
Single
Il metodo consiste nel trovare i singleton nella tabella, ad es. celle in cui è possibile solo una cifra e nessun'altra. Scriviamo questo numero in questa cella e lo escludiamo da altre celle in questa riga, colonna e blocco. Ad esempio: in questa tabella ci sono tre “singoli” (sono evidenziati in giallo).

Single nascosti
Se in una cella sono presenti più candidati, ma uno di essi non appare in nessun'altra cella di una determinata riga (colonna o blocco), tale candidato viene chiamato "singleton nascosto". Nell'esempio seguente, il candidato "4" nel blocco verde si trova solo nella cella centrale. Ciò significa che ci sarà sicuramente un “4” in questa cella. Inseriamo "4" in questa cella e lo cancelliamo dalle altre celle della 2a colonna e della 5a riga. Allo stesso modo, nella colonna gialla, il candidato “2” si presenta una volta, quindi inseriamo “2” in questa cella ed escludiamo “2” dalle celle della settima riga e dal blocco corrispondente.

I due metodi precedenti sono gli unici metodi che determinano in modo univoco il contenuto di una cella. I seguenti metodi consentono solo di ridurre il numero di candidati nelle celle, il che prima o poi porterà a singleton o singleton nascosti.
Candidato bloccato
Ci sono momenti in cui un candidato all'interno di un blocco si trova solo in una riga (o in una colonna). Dato che una di queste celle conterrà necessariamente questo candidato, questo candidato può essere escluso da tutte le altre celle in una determinata riga (colonna).
Nell'esempio seguente, il blocco centrale contiene il candidato "2" solo nella colonna centrale (celle gialle). Ciò significa che una di queste due celle deve essere sicuramente "2" e nessun'altra cella in quella riga al di fuori di questo blocco può essere "2". Pertanto, "2" può essere escluso come candidato dalle altre celle di questa colonna (celle in verde).

Coppie aperte
Se due celle in un gruppo (riga, colonna, blocco) contengono una coppia candidata identica e nient'altro, nessun'altra cella in quel gruppo può avere il valore di quella coppia. Questi 2 candidati possono essere esclusi da altre cellule del gruppo. Nell'esempio seguente, i candidati "1" e "5" nelle colonne otto e nove formano una coppia aperta all'interno del blocco (celle gialle). Pertanto, poiché una di queste celle deve essere "1" e l'altra deve essere "5", i candidati "1" e "5" vengono esclusi da tutte le altre celle di questo blocco (celle verdi).

Lo stesso può essere formulato per 3 e 4 candidati, rispettivamente partecipano già solo 3 e 4 celle. Triple aperte: dalle celle verdi escludiamo i valori delle celle gialle.

Quattro aperti: dalle celle verdi escludiamo i valori delle celle gialle.

Coppie nascoste
Se due celle in un gruppo (riga, colonna, blocco) contengono candidati che includono una coppia identica che non si trova in nessun'altra cella di quel blocco, allora nessun'altra cella in quel gruppo può avere il valore di quella coppia. Pertanto, tutti gli altri candidati di queste due celle possono essere eliminati. Nell'esempio seguente, i candidati “7” e “5” nella colonna centrale si trovano solo nelle celle gialle, il che significa che tutti gli altri candidati di queste celle possono essere esclusi.

Allo stesso modo, puoi cercare tre e quattro nascosti.
X-Wing
Se un valore ha solo due posizioni possibili in una riga (colonna), deve essere assegnato a una di quelle celle. Se esiste un'altra riga (colonna) in cui lo stesso candidato può trovarsi anche solo in due celle e le colonne (righe) di queste celle coincidono, allora nessuna altra cella di queste colonne (righe) può contenere questa cifra. Diamo un'occhiata ad un esempio:

Nella quarta e quinta riga, il numero “2” può apparire solo in due celle gialle e queste celle si trovano nelle stesse colonne. Pertanto il numero “2” può essere scritto solo in due modi: 1) se nella 5a colonna della 4a riga si scrive “2”, allora dalle celle gialle va escluso il “2” e quindi la posizione “2” ” nella 5a riga è determinato unicamente dalla 7a colonna.

2) se nella 7a colonna della 4a riga si scrive “2”, allora dalle celle gialle si deve escludere “2” e quindi nella 5a riga la posizione del “2” è determinata univocamente dalla 5a colonna.

Pertanto la 5a e la 7a colonna avranno sicuramente il numero “2” o nella 4a riga o nella 5a. Quindi il numero “2” può essere escluso dalle altre celle di queste colonne (celle verdi).
"Pesce spada"
Questo metodo è una variazione del metodo.
Le regole del puzzle stabiliscono che se un candidato si trova su tre righe e solo su tre colonne, nelle altre righe quel candidato in quelle colonne può essere eliminato.
Algoritmo:
- Cerchiamo righe in cui il candidato appare non più di tre volte, ma allo stesso tempo appartiene esattamente a tre colonne.
- Escludiamo il candidato in queste tre colonne dalle altre righe.
La stessa logica si applica nel caso di tre colonne, dove il candidato è limitato a tre righe.
Diamo un'occhiata a un esempio. In tre righe (3, 5 e 7), il candidato “5” appare non più di tre volte (le celle sono evidenziate in giallo). Inoltre, appartengono solo a tre colonne: 3, 4 e 7. Secondo il metodo Swordfish, il candidato “5” può essere escluso dalle altre celle di queste colonne (celle verdi).

Nell'esempio seguente viene utilizzato anche il metodo “Pesce spada”, ma per il caso di tre colonne. Escludiamo il candidato “1” dalle celle verdi.

"X-wing" e "pesce spada" possono essere generalizzati al caso di quattro righe e quattro colonne. Questo metodo si chiamerà “Medusa”.
Colori
Ci sono situazioni in cui un candidato appare solo due volte in un gruppo (in una riga, colonna o blocco). Quindi il numero richiesto sarà sicuramente in uno di essi. La strategia del metodo Colori consiste nel visualizzare questa relazione utilizzando due colori, ad esempio giallo e verde. In questo caso, la soluzione può trovarsi in celle di un solo colore.
Selezioniamo tutte le catene interconnesse e prendiamo una decisione:
- Se un candidato non ombreggiato ha due vicini di colore diverso in un gruppo (riga, colonna o blocco), può essere escluso.
- Se in un gruppo (riga, colonna o blocco) sono presenti due colori identici, quel colore è falso. Un candidato da tutte le celle di questo colore può essere eliminato.
L'esempio seguente applica il metodo Colors alle celle con il candidato "9". Iniziamo a colorare dalla cella nel blocco in alto a sinistra (2a riga, 2a colonna), dipingiamola di giallo. Nel suo blocco ha un solo vicino con “9”, dipingiamolo di verde. Inoltre ha un solo vicino nella colonna, quindi dipingiamo anche quello di verde.


Lavoriamo allo stesso modo con le restanti celle contenenti il numero “9”. Noi abbiamo:

Il candidato "9" può trovarsi solo in tutte le celle gialle o in tutte le celle verdi. Nel blocco centrale destro ci sono due celle dello stesso colore, quindi il colore verde non è corretto, poiché in questo blocco ci sono due “9”, il che non è accettabile. Escludiamo "9" da tutte le celle verdi.

Un altro esempio sul metodo “Colori”. Contrassegniamo le celle accoppiate per il candidato "6".

La cella con “6” nel blocco centrale superiore (evidenziata in lilla) ha due candidati di colore diverso:

Il “6” si troverà sicuramente in una cella gialla o verde, quindi il “6” può essere escluso da questa cella lilla.
Un puzzle matematico chiamato "" viene dal Giappone. È diventato diffuso in tutto il mondo per il suo fascino. Per risolverlo, dovrai concentrare la tua attenzione, memoria e usare il pensiero logico.
Il puzzle è pubblicato su giornali e riviste; esistono versioni per computer del gioco e applicazioni mobili. L'essenza e le regole in ognuno di essi sono le stesse.
Come giocare
Il puzzle è basato su un quadrato latino. Il campo di gioco ha la forma di questa particolare figura geometrica, ciascun lato del quale è composto da 9 celle. Il quadrato grande è riempito di piccoli blocchi quadrati, sottoquadrati, con un lato di tre quadrati. All'inizio del gioco, su alcuni di essi sono già scritti dei numeri “suggerimento”.
È necessario riempire tutte le celle vuote rimanenti con numeri naturali da 1 a 9.
Questo deve essere fatto in modo che i numeri non si ripetano:
- in ogni colonna,
- in ogni riga,
- in uno qualsiasi dei quadratini.
Pertanto, in ogni riga e in ogni colonna del quadrato grande ci saranno dei numeri da uno a dieci, anche ogni quadrato piccolo conterrà questi numeri senza ripetizione.
Livelli di difficoltà
Il gioco ha una sola soluzione corretta. Esistono diversi livelli di difficoltà: un semplice puzzle, con un gran numero di celle piene, può essere risolto in pochi minuti. Uno complesso, in cui vengono inseriti un numero limitato di numeri, può richiedere diverse ore.
Tecniche di soluzione
Vengono utilizzati vari approcci per risolvere i problemi. Diamo un'occhiata a quelli più comuni.
Metodo di eliminazione
Questo è un metodo deduttivo, implica la ricerca di opzioni inequivocabili, quando solo una cifra è adatta per scrivere in una cella.
Prima di tutto, prendiamo il quadrato più pieno di numeri, quello in basso a sinistra. Manca uno, sette, otto e nove. Per sapere dove metterlo, diamo un'occhiata alle colonne e alle righe dove si trova questo numero: è nella seconda colonna, quindi la nostra cella vuota (quella più in basso nella seconda colonna) non può contenerlo. Ciò lascia tre possibili opzioni. Ma anche la riga inferiore e la seconda riga dal basso contengono uno - quindi, con il metodo di eliminazione, ci rimane la cella vuota in alto a destra nel sottoquadrato in questione.
Allo stesso modo, riempi tutte le celle vuote.
Scrivere i numeri candidati in una cella
Per risolvere il problema, le opzioni - i numeri dei candidati - vengono scritte nell'angolo in alto a sinistra della cella. Quindi i “candidati” che non soddisfano le regole del gioco vengono eliminati. In questo modo, tutto lo spazio libero viene gradualmente riempito.
I giocatori esperti competono tra loro in abilità e velocità nel riempire le celle vuote, anche se è meglio risolvere questo puzzle lentamente - e quindi completare con successo il Sudoku porterà grande soddisfazione.
Il Sudoku è un puzzle interessante per allenare la logica, a differenza dei puzzle con parole scansionate, che richiedono erudizione e memoria. Il sudoku ha molti paesi d'origine, in un modo o nell'altro veniva giocato nell'antica Cina, in Giappone, in Nord America... Per permetterci di imparare il gioco, abbiamo fatto una selezione Come risolvere il Sudoku da facile a difficile.
Per cominciare diciamo che il Sudoku è un quadrato di 9x9, che a sua volta è composto da 9 quadrati di 3x3. Ogni quadrato deve essere riempito con numeri da uno a nove in modo che ogni numero venga utilizzato solo una volta lungo una linea verticale e orizzontale e solo in un quadrato 3x3.
Quando riempi tutte le celle, dovresti avere tutti i numeri da 1 a 9 in ciascuno dei 9 quadrati. Quindi, lungo la linea orizzontale tutti i numeri sono da 1 a 9. E lungo la linea verticale la stessa cosa, vedi la foto:
Sembrerebbe che queste siano regole semplici, ma per rispondere alla domanda su come risolvere il Sudoku, e ancora di più, se vuoi sapere come risolvere il Sudoku complesso (soprattutto per coloro che hanno appena iniziato il loro viaggio), tu è necessario risolvere almeno un paio di problemi facili. Allora sarà chiaro di cosa stiamo parlando. Di seguito i giochi. Prova a stamparli e compilarli in modo che tutto combacia:


Come risolvere il Sudoku difficile
Spero che tu abbia letto il testo sopra e risolto il compito di cui hai bisogno per capire cosa verrà discusso dopo. Se sì, allora continuiamo.
Questa parte dell'articolo risponderà alle domande:
Come risolvere il Sudoku difficile?
Come risolvere il Sudoku: metodi?
Come risolvere il Sudoku: metodi e metodi di celle e campi?
Quindi, ti sono stati dati due giochi, risolvendoli hai acquisito abilità e ti sei fatto un'idea generale. Per risparmiare tempo, ti dirò un paio di trucchetti per risolvere rapidamente il Sudoku.
1. Inizia sempre dal numero 1 e procedi prima lungo le linee e poi lungo i quadrati. In questo modo sicuramente non ti confonderai ed eviterai di commettere molti errori.
2. Controlla sempre quale numero manca dove sono rimaste meno celle vuote. Ciò farà risparmiare tempo. E assicurati di prestare attenzione a quanti e quali numeri mancano nel quadrato 3 per 3 (sia linee orizzontali che verticali).
3. Se ci sono molte celle vuote in un quadrato e raggiungi un vicolo cieco, prova a dividere il quadrato lungo delle linee nella tua mente. Pensa a quali numeri potrebbero esserci, e da questo potrai capire quali numeri saranno sulle stesse righe in altri quadrati (e forse anche capire quali numeri saranno in altri quadrati su un'altra riga).
4. Non aver paura di nulla, è meglio sbagliare e capire il perché che non fare nulla!
5. Ancora pratica e diventerai un maestro.
E se le persone che risolvono il Sudoku possiedono anche un'intelligenza astratta, che dà un potente potenziale al suo proprietario, allora si può andare molto avanti. Leggi di più su queste persone.
Di seguito troverai una selezione di “Come risolvere il Sudoku difficile”, dopodiché potrai fare moltissimo!



Il Sudoku è un puzzle molto interessante. È necessario disporre i numeri da 1 a 9 nel campo in modo che ogni riga, colonna e blocco di 3 x 3 celle contenga tutti i numeri e allo stesso tempo non si ripetano. Diamo un'occhiata alle istruzioni passo passo su come giocare a Sudoku, ai metodi di base e alla strategia di soluzione.
Algoritmo risolutivo: dal semplice al complesso
L'algoritmo per risolvere il gioco mentale del Sudoku è abbastanza semplice: devi ripetere i seguenti passaggi fino a quando il problema non sarà completamente risolto. Passa gradualmente dai passaggi più semplici a quelli più complessi, quando i primi non consentono più di aprire una cella o escludere un candidato.
Candidati singoli
Innanzitutto, per una spiegazione più chiara di come si gioca a Sudoku, introdurremo un sistema di numerazione dei blocchi e delle celle del campo. Sia le celle che i blocchi sono numerati dall'alto verso il basso e da sinistra a destra.
Cominciamo a guardare il nostro campo. Per prima cosa devi trovare singoli candidati per un posto nella cella. Possono essere nascosti o evidenti. Diamo un'occhiata ai possibili candidati per il sesto blocco: vediamo che solo una delle cinque celle libere contiene un numero univoco, quindi quattro possono essere tranquillamente inseriti nella quarta cella. Considerando ulteriormente questo blocco, possiamo concludere: la seconda cella deve contenere il numero 8, poiché dopo aver eliminato il quattro, l'otto non compare in nessun'altra parte del blocco. Con la stessa giustificazione mettiamo il numero 5.

Esamina attentamente tutte le opzioni possibili. Osservando la cella centrale del quinto blocco, scopriamo che oltre al numero 9 non possono esserci altre opzioni: questo è un chiaro candidato unico per questa cella. Nove possono essere cancellati dalle celle rimanenti di questo blocco, dopodiché i numeri rimanenti possono essere facilmente inseriti. Usando lo stesso metodo, esaminiamo le celle di altri blocchi.
Come individuare le “coppie nude” nascoste ed evidenti
Inseriti i numeri necessari nel quarto blocco, torniamo alle celle vuote del sesto blocco: è ovvio che nella terza cella dovrebbe esserci il numero 6 e nella nona 9.

Il concetto di "coppia nuda" è presente solo nel gioco Sudoku. Le regole per il loro rilevamento sono le seguenti: se due celle dello stesso blocco, riga o colonna contengono una coppia identica di candidati (e solo questa coppia!), allora le restanti celle del gruppo non possono averli. Spieghiamolo utilizzando l'ottavo blocco come esempio. Avendo inserito i possibili candidati in ciascuna cella, troviamo una chiara “coppia nuda”. I numeri 1 e 3 sono presenti nella seconda e nella quinta cella di questo blocco, e in ciascuna ci sono solo 2 candidati, quindi possono essere tranquillamente esclusi dalle celle rimanenti.

Completare il puzzle
Se hai imparato la lezione su come giocare a Sudoku e hai seguito le istruzioni sopra passo dopo passo, dovresti ritrovarti con un'immagine simile a questa:

Qui puoi trovare singoli candidati: uno nella settima cella del nono blocco e un due nella quarta cella del terzo blocco. Prova a risolvere il puzzle fino alla fine. Ora confronta il risultato con la soluzione corretta.

Accaduto? Congratulazioni, perché questo significa che hai imparato con successo le lezioni su come giocare a Sudoku e imparato a risolvere semplici enigmi. Esistono molte varietà di questo gioco: Sudoku di diverse dimensioni, Sudoku con aree aggiuntive e condizioni aggiuntive. Il campo di gioco può variare da 4 x 4 a 25 x 25 celle. Potresti imbatterti in un puzzle in cui i numeri non possono essere ripetuti in un'area aggiuntiva, ad esempio in diagonale.
Inizia con opzioni semplici e passa gradualmente a quelle più complesse, perché con la formazione arriva l'esperienza.
La prima cosa che dovrebbe essere decisa nella metodologia di problem solving è la questione di comprendere effettivamente cosa otteniamo e cosa possiamo ottenere in materia di problem solving. La comprensione è solitamente data per scontata e perdiamo di vista il fatto che la comprensione ha un certo punto di partenza della comprensione, solo in relazione al quale possiamo dire che la comprensione avviene effettivamente a partire da un momento specifico da noi determinato. Il sudoku qui, a nostro avviso, è conveniente in quanto ci consente di modellare, in una certa misura, problemi di comprensione e risoluzione dei problemi. Inizieremo però con esempi leggermente diversi e non meno importanti del Sudoku.
Un fisico che studia la relatività speciale può parlare delle proposizioni “cristalline” di Einstein. Mi sono imbattuto in questa frase su uno dei siti su Internet. Ma da dove inizia questa comprensione della “chiarezza cristallina”? Inizia con l'assimilazione della notazione matematica dei postulati, da cui tutte le strutture matematiche a più piani di SRT possono essere costruite secondo regole conosciute e comprensibili. Ma ciò che il fisico, come me, non capisce è perché i postulati della SRT funzionano in questo particolare modo e non altrimenti.
Innanzitutto, la stragrande maggioranza di coloro che discutono questa dottrina non capiscono cosa contenga esattamente il postulato della costanza della velocità della luce tradotto dalla sua applicazione matematica alla realtà. E questo postulato implica la costanza della velocità della luce in tutti i sensi concepibili e inconcepibili. La velocità della luce è costante rispetto a qualsiasi oggetto fermo e in movimento contemporaneamente. La velocità di un raggio luminoso, secondo il postulato, è costante anche rispetto al raggio luminoso incidente, trasversale e allontanante. E, allo stesso tempo, in realtà abbiamo solo misurazioni indirettamente legate alla velocità della luce, interpretata come la sua costanza.
Le leggi di Newton sono così familiari a un fisico e anche a chi semplicemente studia fisica che sembrano così comprensibili, come qualcosa di evidente e non può essere altrimenti. Ma, diciamo, l'applicazione della legge di gravitazione universale inizia con la sua notazione matematica, dalla quale si possono calcolare anche le traiettorie degli oggetti spaziali e le caratteristiche delle orbite. Ma non abbiamo una tale comprensione del motivo per cui queste leggi funzionano in questo modo e non altrimenti.
Lo stesso con il Sudoku. Su Internet puoi trovare descrizioni ripetute di modi “base” per risolvere i problemi di Sudoku. Se ricordi queste regole, puoi capire come si risolve questo o quel problema del Sudoku applicando le regole “base”. Ma ho una domanda: capiamo perché questi metodi “base” funzionano così e non altrimenti.
Passiamo quindi al successivo punto chiave della metodologia di problem solving. La comprensione è possibile solo sulla base di un qualche tipo di modello che fornisce una base per questa comprensione e l'opportunità di condurre qualche esperimento naturale o mentale. Senza questo, possiamo avere solo regole per applicare i punti di partenza memorizzati: i postulati dell'SRT, le leggi di Newton o i metodi "base" del Sudoku.
Non abbiamo e, in linea di principio, non possiamo avere modelli che soddisfino il postulato della costanza illimitata della velocità della luce. Non ne abbiamo, ma si possono inventare modelli non dimostrabili coerenti con le leggi di Newton. E ci sono modelli "newtoniani", ma in qualche modo non impressionano con le loro capacità produttive per condurre un esperimento su vasta scala o mentale. Ma il Sudoku ci offre opportunità che possiamo utilizzare sia per comprendere i problemi stessi del Sudoku sia per illustrare la modellazione come approccio generale alla risoluzione dei problemi.
Un possibile modello per i problemi di Sudoku è un foglio di lavoro. Viene creato semplicemente riempiendo tutte le celle vuote (celle) della tabella specificata nel problema con i numeri 123456789. Successivamente, l'attività si riduce alla rimozione sequenziale di tutte le cifre extra dalle celle finché tutte le celle della tabella non vengono riempite con singole cifre (esclusive) che soddisfano le condizioni del problema.
Creo un foglio di lavoro di questo tipo in Excel. Per prima cosa seleziono tutte le celle vuote (celle) della tabella. Premo F5 - "Seleziona" - "Celle vuote" - "OK". Un modo più generale per selezionare le celle richieste: tieni premuto Ctrl e fai clic con il mouse per selezionare queste celle. Quindi per le celle selezionate ho impostato il colore blu, la dimensione 10 (iniziale - 12) e il carattere Arial Narrow. Tutto questo in modo che le successive modifiche nella tabella siano chiaramente visibili. Successivamente, inserisco i numeri 123456789 nelle celle vuote. Lo faccio come segue: scrivo e salvo questo numero in una cella separata. Quindi premo F2, seleziono e copio questo numero usando Ctrl+C. Successivamente, vado alle celle della tabella e, esaminando in sequenza tutte le celle vuote, inserisco in esse il numero 123456789 utilizzando l'operazione Ctrl + V e la tabella di lavoro è pronta.
Rimuovo i numeri extra, di cui parleremo più avanti, come segue. Utilizzando l'operazione Ctrl+clic, seleziono le celle con un numero aggiuntivo. Quindi premo Ctrl+H e inserisco il numero da eliminare nel campo superiore della finestra che si apre, mentre il campo inferiore dovrebbe essere completamente vuoto. Successivamente, fai semplicemente clic sull'opzione "Sostituisci tutto" e la cifra extra verrà eliminata.
A giudicare dal fatto che di solito riesco a eseguire elaborazioni di tabelle più avanzate nei soliti modi "di base" rispetto agli esempi forniti su Internet, il foglio di lavoro è lo strumento più semplice per risolvere i problemi di Sudoku. Inoltre, molte situazioni riguardanti l'applicazione delle regole più complesse, dette “base”, semplicemente non si presentavano nel mio foglio di lavoro.
Allo stesso tempo, il foglio di lavoro è anche un modello sul quale è possibile condurre esperimenti con la successiva identificazione di tutte le regole “base” e delle varie sfumature della loro applicazione derivanti dagli esperimenti.
Quindi, ecco un frammento di un foglio di lavoro con nove blocchi, numerati da sinistra a destra e dall'alto verso il basso. In questo caso, abbiamo il quarto blocco riempito con i numeri 123456789. Questo è il nostro modello. All'esterno del blocco, abbiamo evidenziato in rosso i numeri “attivati” (finalmente determinati), in questo caso i quattro, che intendiamo inserire nella tabella in corso di compilazione. I cinque blu sono numeri che non sono ancora stati determinati riguardo al loro ruolo futuro, di cui parleremo più avanti. I numeri attivati che abbiamo assegnato sono, per così dire, barrati, espulsi, cancellati - in generale, sostituiscono i numeri con lo stesso nome nel blocco, quindi sono rappresentati lì in un colore pallido, a simboleggiare il fatto che questi i numeri pallidi vengono cancellati. Volevo rendere questo colore ancora più chiaro, ma poi potrebbero diventare completamente invisibili se visualizzati su Internet.
Di conseguenza, nel quarto blocco nella cella E5 ce n'era uno, anch'esso attivato, ma nascosto quattro. “Attivato” perché a sua volta può rimuovere anche le cifre non necessarie se ne compaiono sul suo percorso, e “nascosto” perché si trova tra altre cifre. Se la cella E5 viene attaccata dai rimanenti, ad eccezione di 4, numeri attivati 12356789, apparirà un singleton "nudo" in E5 - 4.
Ora rimuoviamo uno dei quattro attivati, ad esempio da F7. Quindi i quattro nel blocco riempito possono finire più stretti e solo nella cella E5 o F5, pur rimanendo attivati nella riga 5. Se i cinque attivati vengono portati in questa situazione, senza F7=4 e F8=5, allora un attivato nudo o nascosto coppia 45.
Dopo aver lavorato e compreso sufficientemente le diverse opzioni con singoli, doppi, tripli nudi e nascosti, ecc. non solo nei blocchi, ma anche nelle righe e nelle colonne, possiamo passare ad un altro esperimento. Creiamo una coppia nuda 45, come fatto prima, e poi colleghiamo F7=4 e F8=5 attivati. Di conseguenza si presenterà la situazione E5=45. Situazioni come questa si verificano molto spesso durante la lavorazione di un foglio di lavoro. Questa situazione significa che una di queste cifre, in questo caso 4 o 5, deve trovarsi nel blocco, riga e colonna che include la cella E5, perché in tutti questi casi devono esserci due cifre, non solo una.
E, cosa più importante, ora sappiamo già con quale frequenza si verificano situazioni come E5=45. Allo stesso modo, definiremo le situazioni in cui compaiono tre cifre in una cella, ecc. E quando portiamo il grado di comprensione e percezione di queste situazioni a uno stato di evidenza e semplicità, allora il passo successivo è, per così dire, una comprensione scientifica delle situazioni: saremo quindi in grado di fare un’analisi statistica delle tabelle Sudoku, identificare schemi e utilizzare il materiale accumulato per risolvere i problemi più complessi.
Così, sperimentando sul modello, otteniamo una rappresentazione visiva e addirittura “scientifica” di singoli, coppie, terzine nascoste o aperte, ecc. Se ti limiti ad operare solo con il semplice modello descritto, alcune delle tue idee risulteranno imprecise o addirittura errate. Tuttavia, non appena si passa alla risoluzione di problemi specifici, le imprecisioni delle idee iniziali diventeranno presto evidenti e i modelli su cui sono stati condotti gli esperimenti dovranno essere ripensati e perfezionati. Questo è il percorso inevitabile di ipotesi e chiarimenti nella risoluzione di eventuali problemi.
Va detto che i singoli nascosti e aperti, così come le coppie aperte, le terzine e persino i quattro, sono situazioni comuni che si verificano quando si risolvono i problemi di Sudoku con un foglio di lavoro. Gli accoppiamenti nascosti erano rari. Ma ecco i tre, i quattro, ecc. nascosti. In qualche modo non mi sono imbattuto durante l'elaborazione dei fogli di lavoro, proprio come i metodi "x-wing" e "pesce spada" per aggirare i contorni, che sono stati ripetutamente descritti su Internet, in cui i "candidati" per la cancellazione si presentano in una qualsiasi delle due alternative metodi per aggirare i contorni. Il significato di questi metodi: se distruggiamo il “candidato” x1, rimane il candidato esclusivo x2 e allo stesso tempo viene eliminato il candidato x3, e se distruggiamo x2, rimane il candidato esclusivo x1, ma in questo caso il candidato anche x3 viene eliminato, quindi in ogni caso x3 dovrebbe essere eliminato, senza influenzare per ora i candidati x1 e x2. Più in generale, questo è un caso particolare della situazione: se due metodi alternativi portano allo stesso risultato, allora quel risultato può essere utilizzato per risolvere un problema di Sudoku. Mi sono imbattuto in situazioni in questo senso più generale, ma non nelle varianti “x-wing” e “pesce spada”, e non durante la risoluzione di problemi di Sudoku, per i quali è sufficiente la conoscenza solo degli approcci “base”.
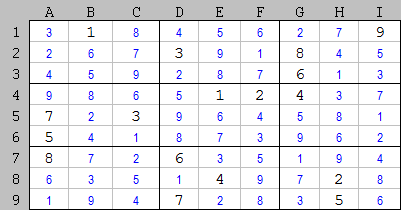
Le caratteristiche dell'utilizzo del foglio di lavoro possono essere mostrate nel seguente esempio non banale. Su uno dei forum dei risolutori di Sudoku http://zforum.net/index.php?topic=3955.25;wap2 mi sono imbattuto in un problema presentato come uno dei problemi di Sudoku più difficili, che non può essere risolto con metodi convenzionali, senza utilizzare forza bruta con ipotesi riguardanti i numeri inseriti nelle celle. Mostreremo che con un foglio di lavoro puoi risolvere questo problema senza una ricerca così esaustiva:

A destra c'è il compito originale, a sinistra c'è il foglio di lavoro dopo la "cancellazione", cioè operazione di routine di rimozione delle cifre extra.
Innanzitutto, concordiamo sulla notazione. ABC4=689 significa che le celle A4, B4 e C4 contengono i numeri 6, 8 e 9 - una o più cifre per cella. È lo stesso con le stringhe. Quindi, B56=24 significa che le celle B5 e B6 contengono i numeri 2 e 4. Il segno ">" è un segno di un'azione condizionata. Quindi D4=5>I4-37 significa che, a causa del messaggio D4=5, il numero 37 dovrebbe essere inserito nella cella I4. Il messaggio può essere esplicito – “nudo” – e nascosto, che deve essere svelato. L'impatto di un messaggio può essere sequenziale (trasmesso indirettamente) lungo la catena o parallelo (impatto diretto su altre cellule). Per esempio:
D3=2; D8=1>A9-1>A2-2>A3-4,G9-3; (D8=1)+(G9=3)>G8-7>G7-1>G5-5
Questa voce significa che D3=2, ma questo fatto deve essere rivelato. D8=1 trasmette la sua influenza ad A3 lungo la catena e 4 va scritto in A3; contemporaneamente D3=2 agisce direttamente su G9, ottenendo il risultato G9-3. (D8=1)+(G9=3)>G8-7 – l’influenza combinata dei fattori (D8=1) e (G9=3) porta al risultato G8-7. E così via.
I record possono contenere anche combinazioni come H56/68. Ciò significa che i numeri 6 e 8 sono vietati nelle celle H5 e H6, ad es. dovrebbero essere rimossi da queste cellule.
Quindi, iniziamo a lavorare con la tabella e applichiamo prima la condizione ben sviluppata e evidente ABC4=689. Ciò significa che in tutte le altre celle (tranne A4, B4 e C4) del blocco 4 (al centro, a sinistra) e della 4a riga i numeri 6, 8 e 9 devono essere rimossi:

Usiamo B56=24 allo stesso modo. In totale abbiamo D4=5 e (dopo D4=5>I4-37) HI4=37, e anche (dopo B56=24>C6-1) C6=1. Applichiamolo al foglio di lavoro:

In I89=68nascosto>I56/68>H56-68: cioè nelle celle I8 e I9 è presente una coppia nascosta di cifre 5 e 6, che vieta la presenza di queste cifre in I56, il che porta al risultato H56-68. Possiamo considerare questo frammento diversamente, proprio come abbiamo fatto negli esperimenti sul modello del foglio di lavoro: (G23=68)+(AD7=68)>I89-68; (I89=68)+(ABC4=689)>H56-68. Cioè, un “attacco” bidirezionale (G23=68) e (AD7=68) porta al fatto che solo i numeri 6 e 8 possono essere in I8 e I9 Next (I89=68) è collegato a “. attacco” su H56 insieme alle condizioni precedenti, che portano a H56-68. Inoltre, (ABC4=689) è collegato a questo “attacco”, che in questo esempio sembra non necessario, tuttavia, se lavorassimo senza un foglio di lavoro, il fattore di impatto (ABC4=689) sarebbe nascosto e sarebbe abbastanza opportuno prestare particolare attenzione ad esso.

Azione successiva: I5=2>G1-2,G6-9,B6-4,B5-2.
Spero sia già chiaro senza commenti: sostituisci i numeri che compaiono dopo il trattino, non sbaglierai:

H7=9>I7-4; D6=8>D1-4,H6-6>H5-8:

La seguente serie di azioni:
D3=2; D8=1>A9-1>A2-2>A3-4,G9-3;
(D8=1)+(G9=3)>G8-7>G7-1>G5-5;
D5=9>MI5-6>FA5-4:

I=4>C9-4>C7-2>E9-2>EF7-35>B7-7,F89-89,
cioè, come risultato della "cancellazione" - rimozione di cifre extra - nelle celle F8 e F9 appare una coppia aperta e "nuda" 89, che, insieme ad altri risultati indicati nella voce, viene applicata alla tabella:

H2=4>H3-1>F2-1>F1-6>A1-3>B8-3,C8-5,H1-7>I2-5>I3-3>I4-7>H4-3
Il loro risultato:

Quindi seguire azioni abbastanza ovvie e di routine:
H1=7>B1-8>B1-5>B3-7>B2-9>B3-8,B3-9>B3-5>B2-6>B2-7>B4-6>A4-9>B4- 8;
SI2=6>SI9-9>LA8-6>I8-8>FA8-9>FA9-8>I9-6;
MI7=3>FA7-5, MI6-7>FA6-3
Il loro risultato: la soluzione finale al problema:
In un modo o nell'altro, supporremo di aver capito i metodi "base" del Sudoku o di altre aree di applicazione intellettuale sulla base di un modello adatto a questo e di aver persino imparato come usarli. Ma questa è solo una parte del nostro progresso nella metodologia di risoluzione dei problemi. Successivamente, ripeto, segue la fase non sempre presa in considerazione, ma indispensabile, di portare i metodi precedentemente appresi a uno stato di facilità d'uso. Risolvere esempi, comprendere i risultati e i metodi di questa soluzione, ripensare questo materiale sulla base del modello adottato, riflettere nuovamente su tutte le opzioni, portare il grado della loro comprensione all'automaticità, quando la soluzione che utilizza le disposizioni "di base" diventa routine e scompare come un problema. Cosa dà questo: tutti dovrebbero sperimentarlo. Ma il punto è che quando una situazione problematica diventa routine, il meccanismo di ricerca dell'intelletto è diretto a padroneggiare disposizioni sempre più complesse nell'ambito dei problemi da risolvere.
Cosa sono le “disposizioni più complesse”? Si tratta solo di nuove disposizioni “fondamentali” per la soluzione del problema, la cui comprensione, a sua volta, può anche essere portata a uno stato di semplicità se si trova un modello adatto a questo scopo.
Nell'articolo Vasilenko S.L. "Number Harmony Sudoku" trovo un esempio di problema con 18 tasti simmetrici:

Per quanto riguarda questo problema, si sostiene che esso può essere risolto utilizzando tecniche “di base” solo fino ad un certo stato, dopodiché non resta che applicare una semplice ricerca con una sostituzione di prova di alcune presunte cifre esclusive (singole, singole) in le cellule. Questo stato (avanzato un po’ oltre rispetto all’esempio di Vasilenko) ha la forma:

Esiste un modello del genere. Questo è un tipo di meccanismo di rotazione per numeri esclusivi (singoli) identificati e non identificati. Nel caso più semplice, un certo trio di cifre esclusive ruota nella direzione destra o sinistra, spostando questo gruppo da riga a riga o da colonna a colonna. In generale, tre gruppi di triple di numeri ruotano in una direzione. Nei casi più complessi, tre coppie di cifre esclusive ruotano in una direzione e una tripla di cifre singole ruota nella direzione opposta. Quindi, ad esempio, vengono ruotate le cifre esclusive nelle prime tre righe del problema in esame. E ciò che è più importante qui è che questo tipo di rotazione può essere notato osservando la disposizione dei numeri nel foglio di lavoro elaborato. Queste informazioni per ora sono sufficienti e comprenderemo altre sfumature del modello di rotazione nel processo di risoluzione del problema.
Quindi, nelle prime tre righe (in alto) (1, 2 e 3) possiamo notare la rotazione delle coppie (3+8) e (7+9), nonché (2+x1) con un x1 sconosciuto e un triplo di singoli (x2+4+1) con incognita x2. Così facendo, possiamo scoprire che ciascuno di x1 e x2 può essere 5 o 6.
Le righe 4, 5 e 6 guardano le coppie (2+4) e (1+3). Dovrebbero esserci anche una terza coppia sconosciuta e una tripla di singoli, di cui si conosce solo un numero, il 5.
Allo stesso modo, esaminiamo la riga 789, quindi le triple delle colonne ABC, DEF e GHI. Annoteremo le informazioni raccolte in una forma simbolica e, spero, abbastanza comprensibile:

Per ora queste informazioni ci servono solo per capire la situazione generale. Rifletteteci attentamente e poi possiamo passare alla seguente tabella appositamente preparata per questo scopo:

Ho evidenziato opzioni alternative con i colori. Il blu significa "consentito" e il giallo significa "vietato". Se, ad esempio, A2=79 è consentito in A2=7, allora C2=7 è proibito. O viceversa – A2=9 è consentito, C2=9 è vietato. E poi autorizzazioni e divieti vengono trasmessi lungo una catena logica. Questa colorazione è stata realizzata per facilitare la visualizzazione delle diverse opzioni alternative. In generale, questa è una sorta di analogia con i metodi "x-wing" e "pesce spada" precedentemente menzionati durante l'elaborazione delle tabelle.
Considerando l'opzione B6=7 e, di conseguenza, B7=9, possiamo immediatamente individuare due punti incompatibili con questa opzione. Se B7=9, nelle righe 789 appare una tripla con rotazione sincrona, il che è inaccettabile, poiché solo tre coppie (e tre singoli in modo asincrono con esse) o tre triple (senza singoli) possono ruotare in modo sincrono (in una direzione). Inoltre, se B7=9, dopo diversi passaggi di elaborazione del foglio di lavoro nella 7a riga troveremo un'incompatibilità: B7=D7=9. Quindi sostituiamo l'unica accettabile delle due opzioni alternative B6 = 9, e quindi il problema viene risolto utilizzando semplici mezzi di elaborazione convenzionale senza alcuna ricerca cieca:

Successivamente, ho un esempio già pronto che utilizza il modello di rotazione per risolvere un problema del Campionato mondiale di Sudoku, ma ometterò questo esempio per non rendere questo articolo troppo lungo. Inoltre, come si è scoperto, questo problema ha tre possibili soluzioni, il che non è adatto allo sviluppo iniziale del modello di rotazione delle cifre. Ho anche passato un bel po' di tempo a riflettere sul problema di Gary McGuire, preso da Internet, con 17 chiavi per risolvere il suo puzzle, finché, con irritazione ancora più notevole, ho scoperto che questo "puzzle" ha più di 9mila soluzioni possibili .
Quindi, volenti o nolenti, dobbiamo passare al problema del Sudoku “più difficile del mondo”, sviluppato da Arto Incala, che, come sappiamo, ha una soluzione unica.
Dopo aver inserito due numeri esclusivi molto ovvi ed aver elaborato il foglio di lavoro, il problema si presenta così:

I tasti assegnati all'attività originale sono evidenziati in nero e con caratteri più grandi. Per andare avanti nella risoluzione di questo problema, dobbiamo ancora una volta fare affidamento su un modello adeguato e adatto a questo scopo. Questo modello è una sorta di meccanismo per ruotare i numeri. È già stato discusso più di una volta in questo e in articoli precedenti, ma per comprendere l'ulteriore materiale dell'articolo, questo meccanismo dovrebbe essere pensato ed elaborato in dettaglio. Più o meno come se avessi lavorato con un meccanismo del genere per dieci anni. Ma sarai comunque in grado di comprendere questo materiale, se non dalla prima lettura, poi dalla seconda o terza, ecc. Inoltre, se mostri tenacia, porterai questo materiale "difficile da comprendere" allo stato della sua routine e semplicità. Non c'è niente di nuovo in questo senso: ciò che all'inizio è molto difficile diventa gradualmente meno difficile, e con l'ulteriore elaborazione continua, tutto ciò che è più evidente e che non richiede sforzo mentale cade al suo posto, dopodiché puoi liberare la tua mente. potenziale mentale per ulteriori progressi rispetto al problema da risolvere o riguardo ad altri problemi.
Dopo un'attenta analisi della struttura del problema Arto Incal, si può notare che è tutto costruito sul principio di tre coppie che ruotano in modo sincrono e tre singoli che ruotano in modo asincrono rispetto alle coppie: (x1+x2)+(x3+x4)+(x5 +x6)+(x7+x8+ x9). L'ordine di rotazione potrebbe, ad esempio, essere il seguente: nelle prime tre righe 123, la prima coppia (x1+x2) si sposta dalla prima riga del primo blocco alla seconda riga del secondo blocco, quindi alla terza riga del terzo blocco. La seconda coppia salta dalla seconda fila del primo blocco alla terza fila del secondo blocco, poi, in questa rotazione, salta alla prima fila del terzo blocco. La terza coppia della terza riga del primo blocco salta nella prima riga del secondo blocco e poi, nello stesso senso di rotazione, entra nella seconda riga del terzo blocco. Il triplo dei singoli si muove in una modalità di rotazione simile, ma in senso opposto alla rotazione delle coppie. La situazione con le colonne è simile: se la tabella viene ruotata mentalmente (o effettivamente) di 90 gradi, le righe diventeranno colonne, con lo stesso schema di movimento dei singoli e delle coppie di prima per le righe.
Eseguendo queste rotazioni nella nostra mente in relazione al problema Arto Incala, arriviamo gradualmente alla comprensione delle ovvie restrizioni sulla scelta delle opzioni per questa rotazione per la terna di righe o colonne selezionata:
Non dovrebbero esserci triplette e coppie rotanti in modo sincrono (nella stessa direzione): tali terzine, in contrasto con la terzina di singoli, saranno chiamate terzine in futuro;
Non dovrebbero esserci coppie asincrone o singoli asincroni;
Non dovrebbero esserci coppie o singoli che ruotano nella stessa direzione (ad esempio, a destra): questa è una ripetizione delle restrizioni precedenti, ma forse sembrerà più comprensibile.
Inoltre, ci sono altre restrizioni:
Non dovrebbe esserci una singola coppia in 9 righe che corrisponda a una coppia in nessuna delle colonne e lo stesso vale per colonne e righe. Questo dovrebbe essere ovvio: perché il fatto stesso che due numeri si trovino sulla stessa riga indica che si trovano in colonne diverse.
Possiamo anche dire che molto raramente si verificano coincidenze di coppie in triplette di righe diverse o una coincidenza simile in triplette di colonne, e anche raramente coincidenze di triplette di singoli in righe e/o colonne, ma queste sono, per così dire, probabilistiche modelli.
Studio dei blocchi 4,5,6.
Nei blocchi 4-6 sono possibili coppie (3+7) e (3+9). Se accettiamo (3+9), otteniamo una rotazione sincrona inaccettabile della tripletta (3+7+9), quindi abbiamo una coppia (7+3). Dopo aver sostituito questa coppia e aver successivo elaborato la tabella con mezzi convenzionali, otteniamo:

Allo stesso tempo, possiamo dire che 5 in B6=5 può essere solo singleton, asincrono (7+3), e 6 in I5=6 è paragenerativo, poiché è nella stessa riga H5=5 nel sesto blocco e, quindi, non può essere sola e può muoversi solo in sincronia con (7+3.

e ha organizzato i candidati per i single in base al numero di volte in cui sono apparsi in questo ruolo in questa tabella:
Se accettiamo che i 2, 4 e 5 più frequenti siano singoli, secondo le regole di rotazione si possono combinare con essi solo le coppie: (7+3), (9+6) e (1+8) - coppia (1 +9) scartato perché nega la coppia (9+6). Inoltre, dopo aver sostituito queste coppie e singoli ed aver ulteriormente elaborato la tabella utilizzando metodi convenzionali, otteniamo:

È così che la tabella si è rivelata indisciplinata: non vuole essere elaborata fino in fondo.
Dovrai sforzarti e notare che nelle colonne ABC c'è una coppia (7+4) e che il 6 si muove in modo sincrono con il 7 in queste colonne, quindi il 6 è un parageneratore, quindi solo nella colonna “C” del 4° blocco sono possibili combinazioni (6+3) +8 oppure (6+8)+3. La prima di queste combinazioni non funziona, poiché nel 7° blocco della colonna “B” apparirà una tripla sincrona non valida: una terzina (6+3+8). Bene, allora, dopo aver sostituito l'opzione (6+8)+3 ed elaborato la tabella nel modo consueto, arriviamo al completamento con successo dell'attività.
Seconda opzione: torniamo alla tabella ottenuta dopo aver individuato la combinazione (7+3)+5 nella riga 456 e passiamo ad esaminare le colonne ABC.

Qui possiamo notare che la coppia (2+9) non può verificarsi in ABC. Altre combinazioni (2+4), (2+7), (9+4) e (9+7) danno una terzina sincrona in A4+A5+A6 e B1+B2+B3, il che è inaccettabile. Rimane una coppia accettabile (7+4). Inoltre, 6 e 5 si muovono in modo sincrono 7, il che significa che sono parageneranti, cioè formare alcune coppie, ma non 5+6.
Facciamo un elenco delle possibili coppie e delle loro combinazioni con i singoli:

La combinazione (6+3)+8 non funziona, perché in caso contrario si formerà una terzina non valida in una colonna (6+3+8), di cui si è già parlato e che potremo verificare ancora una volta controllando tutte le opzioni. Tra i candidati ai singoli, il numero 3 ottiene il maggior numero di punti e la più probabile tra tutte le combinazioni indicate è: (6+8)+3, cioè (C4=6 + C5=8) + C6=3, che dà:

Successivamente, il candidato più probabile per l'assolo è 2 o 9 (6 punti ciascuno), tuttavia, in ognuno di questi casi, il candidato 1 (4 punti) rimane valido. Cominciamo con (5+29)+1, dove 1 è asincrono con 5, cioè Mettiamo 1 di B5=1 come singleton asincrono in tutte le colonne ABC:

Nel blocco 7, colonna A, le uniche opzioni possibili sono (5+9)+3 e (5+2)+3. Ma è meglio prestare attenzione al fatto che nelle righe 1-3 ora compaiono le coppie (4+5) e (8+9). La loro sostituzione porta a un risultato rapido, ad es. per completare l'attività dopo aver elaborato la tabella utilizzando i mezzi normali.
Bene, ora, dopo aver fatto pratica con le opzioni precedenti, possiamo provare a risolvere il problema Arto Incal senza utilizzare stime statistiche.
Torniamo nuovamente alla posizione di partenza:

Nei blocchi 4-6 sono possibili coppie (3+7) e (3+9). Se accettiamo (3+9), otteniamo una rotazione sincrona inaccettabile della tripletta (3+7+9), quindi per la sostituzione nella tabella abbiamo solo l'opzione (7+3):

5 qui, come vediamo, è singolo, 6 è paraformante. Opzioni valide in ABC5: (2+1)+8, (2+1)+9, (8+1)+9, (8+1)+2, (9+1)+8, (9+1) +2. Ma (2+1) è asincrono (7+3), quindi ciò che rimane è (8+1)+9, (8+1)+2, (9+1)+8, (9+1)+2. In ogni caso 1 è sincrono (7+3) e quindi paragenerante. Sostituiamo 1 in questa veste nella tabella:

Il numero 6 qui è un parageneratore nel blocco. 4-6, ma la coppia cospicua (6+4) non è nell'elenco delle coppie valide. Pertanto, il quattro in A4=4 è asincrono 6:

Poiché D4+E4=(8+1) e secondo l'analisi della rotazione forma questa coppia, otteniamo:

Se le celle C456=(6+3)+8, allora B789=683, cioè otteniamo una terzina sincrona, quindi ci rimane l'opzione (6+8)+3 e il risultato della sua sostituzione:

B2=3 è un singleton qui, C1=5 (asincrono 3) è paragenerante, A2=8 è anche paragenerante. B3=7 può essere sia sincrono che asincrono. Ora possiamo metterci alla prova con tecniche più complesse. Con un occhio allenato (o almeno controllando su un computer), vediamo che per qualsiasi stato B3=7 - sincrono o asincrono - otteniamo lo stesso risultato A1=1. Possiamo quindi sostituire questo valore in A1 e poi, utilizzando mezzi semplici e più comuni, completare il nostro compito, o meglio quello di Arto Incala:

In un modo o nell'altro, abbiamo potuto considerare e persino illustrare tre approcci generali alla risoluzione dei problemi: determinare il punto di comprensione del problema (non speculativo o dichiarato ciecamente, ma un momento reale, a partire dal quale possiamo parlare di comprensione del problema), scegliere un modello che permetta di realizzare la comprensione attraverso un esperimento naturale o mentale e – questo è il terzo – di portare il grado di comprensione e di percezione dei risultati raggiunti ad uno stato di evidenza e semplicità. Esiste anche un quarto approccio, che utilizzo personalmente.
Ogni persona sperimenta stati in cui i compiti intellettuali e i problemi che deve affrontare vengono risolti più facilmente di quanto non avvenga normalmente. Queste condizioni possono essere completamente riprodotte. Per fare questo, devi padroneggiare la tecnica di spegnere i pensieri. Prima, almeno per una frazione di secondo, poi, allungando sempre più questo momento di spegnimento. Non posso aggiungere altro, o meglio consigliare, nulla a riguardo, perché la durata dell’utilizzo di questo metodo è una questione puramente personale. Ma a volte ricorro a questo metodo per molto tempo, quando mi trovo di fronte a un problema per il quale non vedo opzioni su come affrontarlo e risolverlo. Di conseguenza, prima o poi dai magazzini della memoria emerge un prototipo adeguato del modello, che chiarisce l'essenza di ciò che deve essere risolto.
Ho risolto il problema di Incal in diversi modi, compresi quelli descritti negli articoli precedenti. E ho sempre, in un modo o nell'altro, utilizzato questo quarto approccio con lo spegnimento e la successiva concentrazione degli sforzi mentali. La soluzione più rapida al problema l'ho ottenuta con una semplice ricerca - il cosiddetto "metodo poke" - utilizzando però solo opzioni "lunghe": quelle che potrebbero portare rapidamente a un risultato positivo o negativo. Altre opzioni hanno assorbito più tempo, perché la maggior parte del tempo è stato dedicato almeno allo sviluppo approssimativo della tecnologia per l'utilizzo di queste opzioni.
Una buona opzione è anche nello spirito del quarto approccio: sintonizzarsi per risolvere i problemi del Sudoku, sostituendo solo un singolo numero in una cella nel processo di risoluzione del problema. Cioè, la maggior parte del compito e dei suoi dati vengono “scorretti” nella mente. Questo è il modo in cui avviene la maggior parte del processo intellettuale di risoluzione dei problemi ed è un'abilità che dovrebbe essere allenata per migliorare le tue capacità di risoluzione dei problemi. Ad esempio, non sono un risolutore di Sudoku professionista. Ho altri compiti. Tuttavia, voglio prefiggermi il seguente obiettivo: acquisire la capacità di risolvere problemi di Sudoku di maggiore complessità, senza un foglio di lavoro e senza ricorrere alla sostituzione di più di un numero in una cella vuota. In questo caso, è consentito qualsiasi metodo per risolvere il Sudoku, inclusa una semplice enumerazione di opzioni.
Non è un caso che ricordo qui l'enumerazione delle opzioni. Qualsiasi approccio alla risoluzione dei problemi del Sudoku comporta nel suo arsenale una serie di determinati metodi, incluso l'uno o l'altro tipo di ricerca. Inoltre, qualsiasi metodo utilizzato nel Sudoku in particolare o nella risoluzione di altri problemi ha una propria area di applicazione effettiva. Pertanto, quando si risolvono problemi di Sudoku relativamente semplici, i più efficaci sono i semplici metodi "di base", descritti in numerosi articoli su questo argomento su Internet, e il più complesso "metodo di rotazione" spesso risulta essere inutile qui, perché complica solo il corso di una soluzione semplice e, allo stesso tempo, che non fornisce nuove informazioni che compaiono durante la soluzione del problema. Ma nei casi più difficili, come nel caso di Arto Incal, il “metodo della rotazione” può giocare un ruolo fondamentale.
Il sudoku nei miei articoli è solo un esempio illustrativo di approcci alla risoluzione dei problemi. Tra i problemi che ho risolto ce ne sono anche di molto più difficili del Sudoku. Ad esempio, modelli computerizzati di caldaie e turbine presenti sul nostro sito web. Non mi dispiacerebbe nemmeno parlare di loro. Ma per ora ho scelto il Sudoku per mostrare in modo abbastanza chiaro ai miei giovani concittadini i possibili percorsi e le fasi di avanzamento verso l'obiettivo finale dei problemi da risolvere.
È tutto per oggi.



