Soluzione grafica di un'equazione quadratica Rafforzare la capacità di costruire grafici di varie funzioni; Sviluppare la capacità di risolvere graficamente le equazioni quadratiche. Argomento: Soluzione grafica di equazioni

Le equazioni con parametri sono giustamente considerate uno dei problemi più difficili della matematica scolastica. Sono proprio questi compiti che anno dopo anno finiscono nell'elenco dei compiti di tipo B e C nell'esame di stato unificato dell'Esame di Stato unificato. Tuttavia, tra il gran numero di equazioni parametriche, ce ne sono alcune che possono essere facilmente risolte graficamente. Consideriamo questo metodo usando l'esempio della risoluzione di diversi problemi.

Trova la somma dei valori interi del numero a per cui l'equazione |x 2 – 2x – 3| = a ha quattro radici.

Soluzione.

Per rispondere alla domanda del problema, costruiamo grafici di funzioni su un piano di coordinate

y = |x 2 – 2x – 3| e y = a.

Grafico della prima funzione y = |x 2 – 2x – 3| si otterrà dal grafico della parabola y = x 2 – 2x – 3 visualizzando simmetricamente rispetto all'asse x quella parte del grafico che si trova al di sotto dell'asse Ox. La parte del grafico situata sopra l'asse x rimarrà invariata.

Facciamolo passo dopo passo. Il grafico della funzione y = x 2 – 2x – 3 è una parabola, i cui rami sono diretti verso l'alto. Per costruire il suo grafico, troviamo le coordinate del vertice. Questo può essere fatto utilizzando la formula x 0 = -b/2a. Quindi x 0 = 2/2 = 1. Per trovare la coordinata del vertice della parabola lungo l'asse delle ordinate, sostituiamo x 0 con il valore risultante nell'equazione della funzione in questione. Otteniamo che y 0 = 1 – 2 – 3 = -4. Ciò significa che il vertice della parabola ha coordinate (1; -4).

Successivamente, è necessario trovare i punti di intersezione dei rami della parabola con gli assi delle coordinate. Nei punti di intersezione dei rami della parabola con l'asse delle ascisse il valore della funzione è zero. Pertanto, risolviamo l'equazione quadratica x 2 – 2x – 3 = 0. Le sue radici saranno i punti richiesti. Per il teorema di Vieta abbiamo x 1 = -1, x 2 = 3.

Nei punti di intersezione dei rami della parabola con l'asse delle ordinate, il valore dell'argomento è zero. Quindi il punto y = -3 è il punto di intersezione dei rami della parabola con l'asse y. Il grafico risultante è mostrato nella Figura 1.

Per ottenere un grafico della funzione y = |x 2 – 2x – 3|, visualizziamo la parte del grafico situata sotto l'asse x simmetricamente rispetto all'asse x. Il grafico risultante è mostrato nella Figura 2.

Il grafico della funzione y = a è una retta parallela all'asse delle ascisse. È illustrato nella Figura 3. Usando la figura, troviamo che i grafici hanno quattro punti comuni (e l'equazione ha quattro radici) se a appartiene all'intervallo (0; 4).

Valori interi del numero a dall'intervallo risultante: 1; 2; 3. Per rispondere alla domanda del problema, troviamo la somma di questi numeri: 1 + 2 + 3 = 6.

Risposta: 6.

Trova la media aritmetica dei valori interi del numero a per cui l'equazione |x 2 – 4|x| – 1| = a ha sei radici.

Iniziamo tracciando la funzione y = |x 2 – 4|x| – 1|. Per fare ciò usiamo l'uguaglianza a 2 = |a| 2 e seleziona il quadrato completo nell'espressione submodulare scritta a destra della funzione:

x2 – 4|x| – 1 = |x| 2 – 4|x| - 1 = (|x| 2 – 4|x| + 4) – 1 – 4 = (|x |– 2) 2 – 5.

Allora la funzione originale avrà la forma y = |(|x| – 2) 2 – 5|.

Per costruire un grafico di questa funzione, costruiamo grafici sequenziali di funzioni:

1) y = (x – 2) 2 – 5 – parabola con vertice nel punto di coordinate (2; -5); (Fig. 1).

2) y = (|x| – 2) 2 – 5 – la parte della parabola costruita nel passo 1, che si trova a destra dell'asse delle ordinate, viene visualizzata simmetricamente a sinistra dell'asse Oy; (Fig. 2).

3) y = |(|x| – 2) 2 – 5| – la parte del grafico costruita al punto 2, che si trova sotto l'asse x, viene visualizzata simmetricamente rispetto all'asse x verso l'alto. (Fig. 3).

Diamo un'occhiata ai disegni risultanti:

Il grafico della funzione y = a è una retta parallela all'asse delle ascisse.

Utilizzando la figura, concludiamo che i grafici delle funzioni hanno sei punti comuni (l'equazione ha sei radici) se a appartiene all'intervallo (1; 5).

Questo può essere visto nella figura seguente:

Troviamo la media aritmetica dei valori interi del parametro a:

(2 + 3 + 4)/3 = 3.

Risposta: 3.

blog.site, quando si copia materiale in tutto o in parte, è richiesto un collegamento alla fonte originale.

Soluzione grafica di equazioni

Giorno d'oro, 2009

introduzione

La necessità di risolvere equazioni quadratiche nell'antichità fu causata dalla necessità di risolvere problemi legati al reperimento delle aree di terreno e con i lavori di scavo militare, nonché con lo sviluppo dell'astronomia e della matematica stessa. I babilonesi furono in grado di risolvere equazioni quadratiche intorno al 2000 a.C. La regola per risolvere queste equazioni, esposta nei testi babilonesi, coincide essenzialmente con quelli moderni, ma non si sa come i babilonesi siano arrivati ​​a questa regola.

Le formule per risolvere le equazioni quadratiche in Europa furono esposte per la prima volta nel Libro dell'Abaco, scritto nel 1202 dal matematico italiano Leonardo Fibonacci. Il suo libro contribuì alla diffusione della conoscenza algebrica non solo in Italia, ma anche in Germania, Francia e altri paesi europei.

Ma la regola generale per risolvere le equazioni quadratiche, con tutte le possibili combinazioni dei coefficienti b e c, fu formulata in Europa solo nel 1544 da M. Stiefel.

Nel 1591 François Viet introdotte formule per la risoluzione di equazioni quadratiche.

Nell'antica Babilonia potevano risolvere alcuni tipi di equazioni quadratiche.

Diofanto di Alessandria E Euclide, Al-Khwarizmi E Omar Khayyam equazioni risolte utilizzando metodi geometrici e grafici.

In seconda media abbiamo studiato le funzioni y = C, y =kx, y =kx+ M, y =X 2,y = –X 2, in terza media - y = √X, y =|X|, y =ascia2 + bx+ C, y =K/ X. Nel libro di testo di algebra della terza media, ho visto funzioni che non mi erano ancora note: y =X 3, y =X 4,y =X 2n, y =X- 2n, y = 3√X, (X– UN) 2 + (sì –B) 2 = R 2 e altri. Esistono regole per costruire grafici di queste funzioni. Mi chiedevo se esistessero altre funzioni che obbediscono a queste regole.

Il mio lavoro è studiare grafici di funzioni e risolvere graficamente equazioni.

1. Quali sono le funzioni?

Il grafico di una funzione è l'insieme di tutti i punti del piano delle coordinate, le cui ascisse sono uguali ai valori degli argomenti e le ordinate sono uguali ai valori corrispondenti della funzione.

La funzione lineare è data dall'equazione y =kx+ B, Dove K E B- alcuni numeri. Il grafico di questa funzione è una linea retta.

Funzione proporzionale inversa y =K/ X, dove k ¹ 0. Il grafico di questa funzione è chiamato iperbole.

Funzione (X– UN) 2 + (y –B) 2 = R2 , Dove UN, B E R- alcuni numeri. Il grafico di questa funzione è un cerchio di raggio r con centro nel punto A ( UN, B).

Funzione quadratica sì= ascia2 + bx+ C Dove UN,B, Con– alcuni numeri e UN¹ 0. Il grafico di questa funzione è una parabola.

L'equazione A2 (UN– X) = X2 (UN+ X) . Il grafico di questa equazione sarà una curva chiamata strofoide.

/>Equazione (X2 + sì2 ) 2 = UN(X2 – sì2 ) . Il grafico di questa equazione è chiamato lemniscata di Bernoulli.

L'equazione. Il grafico di questa equazione è chiamato astroide.

Curva (X2 sì2 – 2 assi)2 =4 a2 (X2 + sì2 ) . Questa curva è chiamata cardioide.

Funzioni: y =X 3 – parabola cubica, y =X 4, y = 1/X 2.

2. Il concetto di equazione e la sua soluzione grafica

L'equazione– un'espressione contenente una variabile.

Risolvi l'equazione- questo significa ritrovare tutte le sue radici, oppure dimostrare che esse non esistono.

Radice dell'equazioneè un numero che, se sostituito in un'equazione, produce un'uguaglianza numerica corretta.

Risoluzione grafica di equazioni permette di trovare il valore esatto o approssimativo delle radici, permette di trovare il numero di radici dell'equazione.

Quando si costruiscono grafici e si risolvono equazioni, vengono utilizzate le proprietà di una funzione, motivo per cui il metodo viene spesso chiamato grafico-funzionale.

Per risolvere l'equazione, la “dividiamo” in due parti, introduciamo due funzioni, costruiamo i relativi grafici e troviamo le coordinate dei punti di intersezione dei grafici. Le ascisse di questi punti sono le radici dell'equazione.

3. Algoritmo per tracciare il grafico di una funzione

Conoscere il grafico di una funzione y =F(X) , puoi costruire grafici di funzioni y =F(X+ M) ,y =F(X)+ l E y =F(X+ M)+ l. Tutti questi grafici sono ottenuti dal grafico della funzione y =F(X) utilizzando la trasformazione del riporto parallelo: a │ M│ unità di scala a destra o a sinistra lungo l'asse x e oltre │ l│ unità di scala verso l'alto o verso il basso lungo un asse sì.

4. Soluzione grafica dell'equazione quadratica

Utilizzando una funzione quadratica come esempio, considereremo la soluzione grafica di un'equazione quadratica. Il grafico di una funzione quadratica è una parabola.

Cosa sapevano gli antichi greci della parabola?

Il simbolismo matematico moderno ha avuto origine nel XVI secolo.

Gli antichi matematici greci non possedevano né il metodo delle coordinate né il concetto di funzione. Tuttavia, hanno studiato in dettaglio le proprietà della parabola. L'ingegnosità degli antichi matematici è semplicemente sorprendente: dopo tutto, potevano usare solo disegni e descrizioni verbali delle dipendenze.

Ha esplorato in modo più approfondito la parabola, l'iperbole e l'ellisse Apollonio di Perga, vissuto nel III secolo a.C. Ha dato nomi a queste curve e ha indicato quali condizioni soddisfano i punti che giacciono su questa o quella curva (dopo tutto, non c'erano formule!).

Esiste un algoritmo per costruire una parabola:

Trovare le coordinate del vertice della parabola A (x0; y0): X=- B/2 UN;

y0=axo2+in0+s;

Trovare l'asse di simmetria della parabola (retta x=x0);

INTERRUZIONE DI PAGINA--

Compiliamo una tabella di valori per la costruzione dei punti di controllo;

Costruiamo i punti risultanti e costruiamo punti che sono simmetrici ad essi rispetto all'asse di simmetria.

1. Usando l'algoritmo, costruiremo una parabola sì= X2 – 2 X– 3 . Ascisse dei punti di intersezione con l'asse X e ci sono radici dell'equazione quadratica X2 – 2 X– 3 = 0.

Esistono cinque modi per risolvere graficamente questa equazione.

2. Dividiamo l'equazione in due funzioni: sì= X2 E sì= 2 X+ 3

3. Dividiamo l'equazione in due funzioni: sì= X2 –3 E sì=2 X. Le radici dell'equazione sono le ascisse dei punti di intersezione della parabola e della retta.

4. Trasforma l'equazione X2 – 2 X– 3 = 0 isolando un quadrato completo in funzioni: sì= (X–1) 2 E sì=4. Le radici dell'equazione sono le ascisse dei punti di intersezione della parabola e della retta.

5. Dividi entrambi i membri dell'equazione termine per termine X2 – 2 X– 3 = 0 SU X, noi abbiamo X– 2 – 3/ X= 0 , dividiamo questa equazione in due funzioni: sì= X– 2, sì= 3/ X. Le radici dell'equazione sono le ascisse dei punti di intersezione della retta e dell'iperbole.

5. Soluzione grafica delle equazioni di gradoN

Esempio 1. Risolvi l'equazione X5 = 3 – 2 X.

sì= X5 , sì= 3 – 2 X.

Risposta: x = 1.

Esempio 2. Risolvi l'equazione 3 √ X= 10 – X.

Le radici di questa equazione sono l'ascissa del punto di intersezione dei grafici di due funzioni: sì= 3 √ X, sì= 10 – X.

Risposta: x = 8.

Conclusione

Osservando i grafici delle funzioni: y =ascia2 + bx+ C, y =K/ X, у = √X, y =|X|, y =X 3, y =X 4,y = 3√X, Ho notato che tutti questi grafici sono costruiti secondo la regola della traslazione parallela rispetto agli assi X E sì.

Utilizzando l'esempio della risoluzione di un'equazione quadratica, possiamo concludere che il metodo grafico è applicabile anche per equazioni di grado n.

I metodi grafici per risolvere le equazioni sono belli e comprensibili, ma non forniscono una garanzia al 100% di risolvere alcuna equazione. Le ascisse dei punti di intersezione dei grafici possono essere approssimative.

In prima media e al liceo continuerò a conoscere altre funzioni. Sono interessato a sapere se tali funzioni obbediscono alle regole del trasferimento parallelo quando costruiscono i loro grafici.

L'anno prossimo vorrei anche considerare la questione della risoluzione grafica dei sistemi di equazioni e disequazioni.

Letteratura

1. Algebra. 7 ° grado. Parte 1. Libro di testo per istituzioni educative / A.G. Mordkovich. M.: Mnemosine, 2007.

2. Algebra. 8 ° grado. Parte 1. Libro di testo per istituzioni educative / A.G. Mordkovich. M.: Mnemosine, 2007.

3. Algebra. 9° grado. Parte 1. Libro di testo per istituzioni educative / A.G. Mordkovich. M.: Mnemosine, 2007.

4. Glazer G.I. Storia della matematica a scuola. Gradi VII-VIII. – M.: Educazione, 1982.

5. Rivista Matematica N. 5 2009; N. 8 2007; N. 23 2008.

6. Soluzione grafica dei siti web di equazioni su Internet: Tol VIKI; stimul.biz/ru; wiki.iot.ru/images; berdsk.edu; pagina 3–6.htm.

ISTITUTO DEL DAGESTAN PER PROFESSIONISTI AVANZATI

CORPO DOCENTE

DIPARTIMENTO DI FISICA E MATEMATICA E ICT

Progetto

sul tema:

« Costruzione e riforma

grafici di funzioni

in un corso di matematica scolastica »

Rabadanova P.A.

insegnante di matematica

MBOU "Scuola secondaria Kochubeyskaya"

Distretto di Tarumovsky

2015

1. Introduzione…………………….….3

2. Capitolo IO. Revisione della letteratura sul tema del progetto………….….5

3. Capitolo II. Parte empirica:

3.1. Metodi di base per convertire i grafici delle funzioni……….….7

3.2. Anche tramandoEfunzioni strane…………….. 10

3.3. Tracciare il grafico della funzione inversa…………... 11

3.4. Deformazione (compressione e allungamento) dei grafici………………….12

3.5.Combinazione di trasferimento, riflessione e deformazione………………......13

4. Compiti per una soluzione indipendente………..…...14

5. Conclusione…………………………15

6. Conclusioni……………………..………17

INTRODUZIONE

La trasformazione dei grafici di funzioni è uno dei concetti matematici fondamentali direttamente correlati alle attività pratiche. I grafici riflettono la variabilità e il dinamismo del mondo reale, le relazioni reciproche di oggetti e fenomeni reali.

La linea funzionale è un argomento di base trattato negli esami di stato principale e unificato.Inoltre, molti concetti matematici vengono esaminati utilizzando metodi grafici. Ad esempio, aquadraticola funzione viene introdotta e studiata in stretta connessione con equazioni e disequazioni quadratiche.Ne consegue cheInsegnare agli studenti come costruire e trasformare grafici di funzioni è uno dei compiti principali dell'insegnamento della matematica a scuola.

Lo studio della funzione consente di trovare informazioni sudominio di definizione e dominio di valore di una funzione, dominioFrequenze decrescenti o crescenti, asintoti, intervallicostanza del segno, ecc. Tuttavia, per costruire un graficopuoi usare molte funzioniutilizzare una serie di metodirendendolo più semplicecostruzione. Pertanto, gli studenti dovranno avere la competenza per costruire grafici utilizzando schemi metodologici.

Quanto sopra determinapertinenza argomenti di ricerca.

Oggetto di studio è lo studio della trasformazione dei grafici a linee funzionali nella matematica scolastica.

Materia di studio - il processo di costruzione e trasformazione dei grafici delle funzioni in una scuola secondaria.

Scopo dello studio: educativo - consiste nell'individuare uno schema metodologico per la costruzione e la trasformazione dei grafici di funzioni;sviluppando - sviluppo del pensiero astratto, algoritmico, logico, immaginazione spaziale;educativo – coltivare la cultura grafica degli scolari, sviluppando capacità di lavoro mentale.

Gli obiettivi hanno portato alla decisione di quanto seguecompiti:

1. Analizzare materiali didattici e metodologici sul problema in studio.

2. Identificare schemi metodologicitrasformare i grafici delle funzioni in un corso di matematica scolastica.

3. Selezionare i metodi e i mezzi più efficacicostruzione e trasformazione di grafici di funzioni nella scuola secondaria, promuovendo: un'assimilazione significativa del materiale educativo; aumentare l'attività cognitiva degli studenti; sviluppo delle proprie capacità creative.

IPOTESI ricerca: la formazione di competenze grafiche nel processo di studio delle funzioni e di coltivare la cultura grafica degli studenti efficace se gli studenti conoscono lo schema metodologico per la costruzione e la trasformazione dei grafici di funzioni in un corso di matematica scolastica.

CAPITOLO IO . REVISIONE DELLA LETTERATURA SUL TEMA DEL PROGETTO.

In preparazione al progetto, abbiamo studiato la seguente letteratura:

Sivashinsky, I. Kh Teoremi e problemi di algebra, funzioni elementari - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funzioni e grafici (tecniche di base) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Matematica elementare - M., 2010 (ristampa). - 590 s.

Kuzmin, M. K. Rappresentazione grafica di una funzione - J. Matematica a scuola. - 2003. - N. 5. - Pag. 61-62.

Shilov G.E. Come costruire grafici? - M., 1982.

Isacco Thanatar. Trasformazioni geometriche di grafici di funzioni - MCNMO, 2012

INSi noti che la capacità di "leggere" il comportamento di una funzione su un determinato insieme utilizzando un grafico viene utilizzata non solo in un corso di matematica, ma anche in qualsiasi attività umana pratica in cui deve affrontare determinate rappresentazioni grafiche delle dipendenze . Pertanto, gli studenti dovrebbero essere in grado di determinare alcune delle sue proprietà dal grafico di una funzione.

Il materiale teorico per la conversione dei grafici è presentato rigorosamente. La tecnica è accompagnata da illustrazioni, disegni, esempi di varia complessità e relative soluzioni, che consentono di approfondire la conoscenza e costruire grafici di funzioni complesse.

Presenta un corso di formazione elettronico, il cui volume e contenuto corrisponde ai requisiti per un corso di matematica delle scuole superiori. Il materiale teorico è supportato da illustrazioni di animazione grafica che forniscono una rappresentazione visiva dell'argomento oggetto di studio. Il corso prevede tre moduli: un modulo per lo studio del materiale teorico, un modulo di autotest e un modulo di controllo delle conoscenze.

Da , , per la parte empirica del progetto sono stati utilizzati schemi metodologici per la costruzione di grafici ed esempi di lavoro indipendente.

Conclusioni al capitolo 1

Lo studio della letteratura didattica e metodologica ha consentito:

1. Individuare lo schema metodologicostudiare, costruire e trasformare grafici di funzioni in un corso di matematica scolastica.

2. Seleziona i metodi e i mezzi più efficacicostruzione e trasformazione di grafici di funzioni nella matematica scolastica,contribuendo:

apprendimento significativo del materiale didattico;

aumentare l'attività cognitiva degli studenti;

sviluppo delle proprie capacità creative.

3. dimostralo La linea funzionale ha un impatto significativo quando si imparano vari concetti in matematica.

Capitolo 2. PARTE EMPIRICA

In questo capitolo esamineremo i metodi principali per trasformare i grafici di funzioni e forniremo schemi metodologici per costruire varie combinazioni di grafici per varie funzioni.

2.1. METODI BASE PER TRASFORMARE LA GRAFICA DI UNA FUNZIONE

Traslazione lungo l'asse delle ordinate

F ( X ) F ( X )+ B .

Perrappresentare graficamente una funzionesì = F( X) + Bseguenteet:

1. rappresentare graficamente la funzionesì= F( X)

2. spostare l'asseascissa a| B| unità fino aB>0 o a| B| mangiareprostrarsi aB < 0. Ottenuto nel nuovo sistema cooril grafico dinat è il grafico di una funzionesì = F( X) + B.

2. Trasferimento lungo assi ascissa

F ( X ) F ( X + UN ) .

sì = F( X+ UN) seguenteet:

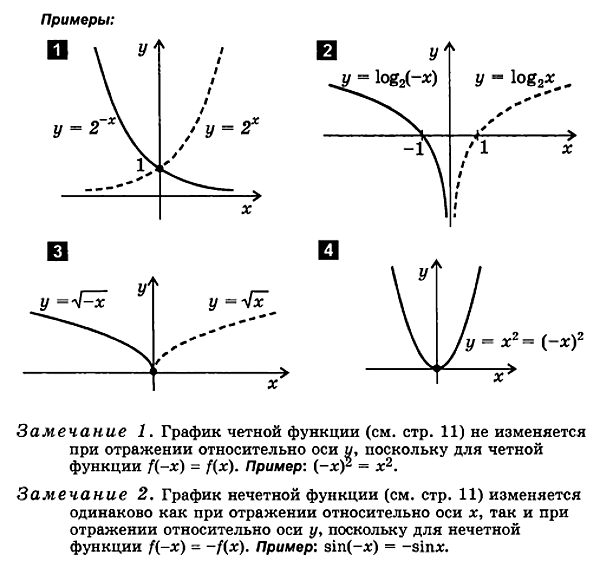
3. Tracciare una funzione del modulo sì = F (- X )

F (X ) F (- X ).

Rappresentare graficamente una funzionesì = F( - x) segue:

rappresentare graficamente una funzionesì = F( X)

rifletterci soprarispetto all'asse y

il grafico risultante ègrafico della funzionesì = F( - X).

4. Tracciare una funzione del modulo y = - F ( X )

F ( X ) - F ( X )

- F( X) segue:

rappresentare graficamente una funzionesì= F( X)

rifletterlo rispetto all'asse x

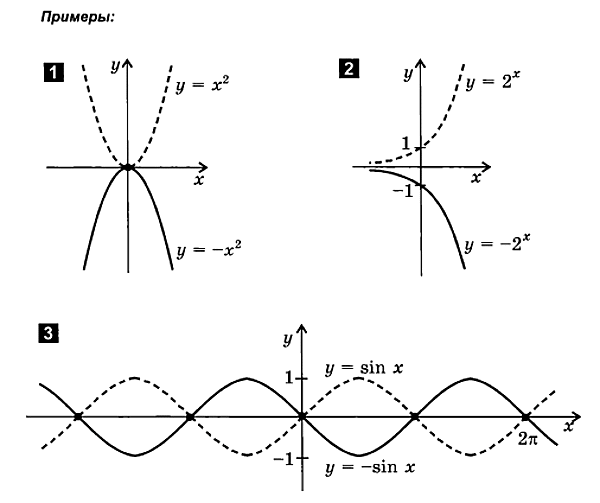
2.2. Anche tramando E funzioni strane

Durante la tramafunzioni pari e dispari, è conveniente utilizzare le seguenti proprietà:

1. Grafico di una funzione di simmetria pariric rispetto all'asse delle ordinate.

2. Il grafico di una funzione dispari è simmetrico rispetto all'origine.

Per tracciare i grafici di una funzione pari e dispari, è sufficiente tracciare solo il ramo destro del grafico per valori positivi dell'argomento. Il ramo di sinistra si completa simmetricamente rispetto all'origine delle coordinate per una funzione dispari e rispetto all'asse delle ordinate per una funzione pari.

Rappresentare graficamente una funzione pari sì = F ( X ) Prossimo colpi:

costruire un ramo del grafico di questa funzione solo in volumeintervallo di valori positivi dell'argomento x≥O.

DItracciare questo ramo rispetto all'asse delle ordinate

Rappresentare graficamente una funzione dispari sì = F ( X ) segue:

costruire un ramo del grafico di questa funzione solo inaree di valori di argomenti positivi (x≥0).

DItracciare questo ramo rispetto all'originealla regione dei valori x negativi.

2.3. Rappresentazione grafica della funzione inversa

Come già notato, le funzioni dirette e inverse turiflettono la stessa relazione tra le variabilixey, con la sola differenza che nella funzione inversa questile variabili si sono scambiate di ruolo, il che equivale a cambiaremodifica delle designazioni degli assi delle coordinate. Quindi il palinsestola funzione inversa è simmetrica al grafico della funzione direttarispetto alla bisettriceIOEIIIangoli di coordinazione,cioè relativamente drittoy = x. Quindi, otteniamoregola successiva.

Per tracciare la funzione y = (x), inverso alla funzionesì = F( X), dovrebbe essere costruitoprogrammasì = F( X) e rifletterlo rispetto alla retta y = x.

2.4. Deformazione (compressione e allungamento) dei grafici

1. Compressione (allungamento) del grafico lungo l'asse delle ordinate

F ( X ) UN ∙ F ( X ).

Rappresentare graficamente una funzionesì= UN∙ F( X) segue:

8. Compressione (allungamento) del grafico lungo l'asse x

F( X)

Per tracciare la funzione y= F( X) segue:

2.5. Combinazione di trasferimento, riflessione e deformazione

Molto spesso quando si costruiscono grafici di funzioni quandomodificare la combinazione delle tecniche.

Applicazione coerente di una serie di tali tecniche di posturaconsente di semplificare notevolmente la costruzione di un grafico utilizzandofunzione in movimento e spesso la riducono alla finecostruzione di una delle funzioni elementari più semplicizioni. Consideriamo come, tenendo conto di quanto sopra, ne conseguecostruire grafici di funzioni.

Tieni presente che è oraSi consiglia di realizzare il documento di semplificazione nella seguente sequenzaness.

Utilizzando parità ofunzione strana.

Trasferimento degli assi.

Riflessione e deformazione.

La costruzione del grafico viene eseguita nell'ordine inverso.

Esempio. Rappresentare graficamente la funzione

Effettueremo la costruzione seguendo le seguenti fasi:

1. costruisci un grafico del logaritmo naturale:

2. spremereall'asseOH2 volte:;
3. visualizzare simmetricamenterispetto all'asseOH: ;
4. muoversi lungo l'asseBUESU(!!!) A destra::

5. visualizzare simmetricamente rispetto all'asseBUE: ;
6. muoviamocilungo l'asseOHfino a 3 unità::

ESEMPI DI COSTRUZIONE E TRASFORMAZIONE DELLA GRAFICA DI UNA FUNZIONE

Esempio 1. Rappresentare graficamente la funzione.

Per prima cosa disegniamo un grafico sinusoidale; il suo periodo è uguale a:

grafico di una funzioneottenuto comprimendo il graficodue volte sull'asse delle ordinate. tronco d'albero .

Rappresentare graficamente la funzioneA = 2 cosX.

Rappresentare graficamente la funzionesì = peccatoX .

CONCLUSIONE

Durante il lavoro sul progetto, è stata analizzata varia letteratura educativa e metodologica su questo problema. I risultati dello studio hanno permesso di identificare gli aspetti positivi più caratteristici dello studio, costruzione e trasformazione di grafici di funzioni in un corso di matematica scolastica

L'obiettivo principale del progetto è sviluppare le capacità degli studenti nella lettura e nel completamento dei disegni e sviluppare metodi razionali di attività indipendente in essi.

La necessità di migliorare l'educazione grafica in generale è dettata non solo dalle moderne esigenze di produzione, ma anche dal ruolo della grafica nello sviluppo del pensiero tecnico e delle capacità cognitive degli studenti. La capacità di una persona di elaborare informazioni grafiche è uno degli indicatori del suo sviluppo mentale. Pertanto, la formazione grafica dovrebbe diventare un elemento integrante della formazione educativa generale.

conclusioni

Pertanto, il progetto sviluppato "Costruzione e trasformazione di grafici di funzioni", dedicato a uno dei concetti centrali della matematica - la dipendenza funzionale, mira a sistematizzare e espandere la conoscenza degli studenti. Lo studio di metodi specifici per la trasformazione dei grafici di funzioni viene effettuato analiticamente e graficamente secondo rigorosi schemi metodologici. Il materiale raccolto potrà essere utilizzato nelle lezioni e per l'autoformazione degli studenti. Per condurre le lezioni possono essere utilizzate varie forme e metodi di organizzazione e formazione.

In questa lezione video viene offerto per lo studio l'argomento "Funzione y=x 2". Soluzione grafica di equazioni." Durante questa lezione, gli studenti potranno conoscere un nuovo modo di risolvere le equazioni: graficamente, che si basa sulla conoscenza delle proprietà dei grafici delle funzioni. L'insegnante mostrerà come risolvere graficamente la funzione y=x 2.

Soggetto:Funzione

Lezione:Funzione. Soluzione grafica di equazioni

La soluzione grafica delle equazioni si basa sulla conoscenza dei grafici delle funzioni e delle loro proprietà. Elenchiamo le funzioni di cui conosciamo i grafici:

1), il grafico è una retta parallela all'asse delle ascisse, passante per un punto sull'asse delle ordinate. Consideriamo un esempio: y=1:

Per valori diversi otteniamo una famiglia di rette parallele all'asse x.

2) Funzione di proporzionalità diretta, il grafico di questa funzione è una retta passante per l'origine delle coordinate. Diamo un'occhiata ad un esempio:

Abbiamo già costruito questi grafici nelle lezioni precedenti; ricordiamo che per costruire ogni retta è necessario selezionare un punto che la soddisfi, e prendere come secondo punto l'origine delle coordinate.

Ricordiamo il ruolo del coefficiente k: al crescere della funzione l'angolo formato dalla retta con la direzione positiva dell'asse x è acuto; quando la funzione decresce, l'angolo formato dalla retta con la direzione positiva dell'asse x è ottuso. Inoltre, tra due parametri k dello stesso segno esiste la seguente relazione: per k positivo, quanto più è grande, tanto più velocemente aumenta la funzione, mentre per quelli negativi la funzione diminuisce più velocemente per grandi valori di k in valore assoluto .

3) Funzione lineare. Quando - otteniamo il punto di intersezione con l'asse delle ordinate e tutte le rette di questo tipo passano per il punto (0; m). Inoltre, all'aumentare della funzione, l'angolo compreso tra la retta e la direzione positiva dell'asse x è acuto; quando la funzione decresce, l'angolo formato dalla retta con la direzione positiva dell'asse x è ottuso. E ovviamente il valore di k influenza la velocità di variazione del valore della funzione.

4). Il grafico di questa funzione è una parabola.

Diamo un'occhiata agli esempi.

Esempio 1 - Risolvi graficamente l'equazione:

Non conosciamo funzioni di questo tipo, quindi dobbiamo trasformare l'equazione data per lavorare con funzioni note:

Otteniamo funzioni familiari su entrambi i lati dell'equazione:

Costruiamo grafici di funzioni:

I grafici hanno due punti di intersezione: (-1; 1); (2; 4)

Controlliamo se la soluzione è stata trovata correttamente e sostituiamo le coordinate nell'equazione:

Il primo punto è stato trovato correttamente.

, , , , , ,

Anche il secondo punto è stato trovato correttamente.

Quindi, le soluzioni dell'equazione sono e

Procediamo in modo simile all'esempio precedente: trasformiamo l'equazione data in funzioni a noi note, costruiamo i loro grafici, troviamo le correnti di intersezione e da qui indichiamo le soluzioni.

Otteniamo due funzioni:

Costruiamo i grafici:

Questi grafici non hanno punti di intersezione, il che significa che l'equazione data non ha soluzioni

Conclusione: in questa lezione abbiamo esaminato le funzioni a noi note e i loro grafici, ricordato le loro proprietà e esaminato il metodo grafico per risolvere le equazioni.

1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. e altri. M.: Illuminazione. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. e altri. Algebra 7.M.: Illuminismo. 2006

Compito 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. e altri.

Compito 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. e altri.

Compito 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. e altri.